
This is the exact shape that home plate and the bases form. In Euclidean geometry, a kite is a quadrilateral whose four sides can be grouped into two pairs of equal length sides that are adjacent to each other. Therefore, if Cannon seeks mathematical precision, the correct term for a baseball field, as represented by home plate and the bases on the field, is a kite. The reason for this is that the center of second base is placed at the exact 90-foot intersection. As a result, half of the width of the base, or 7 1 / 2 inches (a standard base is 15 inches wide), is actually outside of the 90-foot square.
The distance from the apex of the pentagon (the pointy part) to the back of first base (closest to right field) is 90 feet. Similarly, the distance from the apex of home plate to the back of third base is 90 feet. However, the distance from the side of first base on the foul line, to the back of second base (facing left field) is 90 feet, 7 1 / 2 inches - the same as the distance from the foul line side of third base to the opposite, back side of second base (facing right field). The reason is that the physical representation of the infield - namely home plate, the two foul lines and the three bases, do not form an exact square. But beyond that, a baseball diamond or baseball square, if you prefer, is not, in fact, a square. George Carlin would have agreed that baseball is a sport of imprecision and subjectivity. I doubt that those who first coined the term “ baseball diamond” had much interest in mathematical precision. In his example, he states that a baseball “diamond” is not a diamond, but a square and that it should be referred to as such.
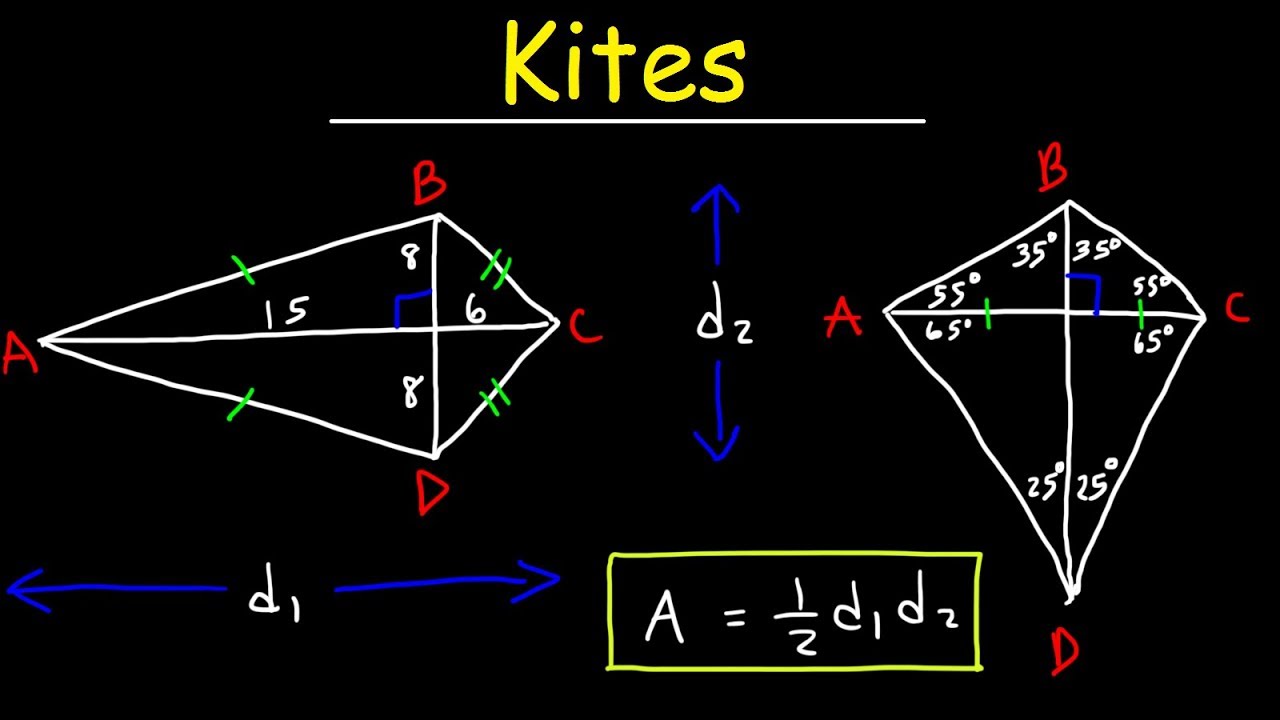
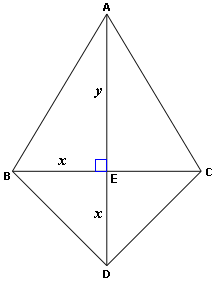
Kite geometry free#
I read James Cannon’s May 26 Free for All letter in which he asks that proper math terms be used to describe a shape.


 0 kommentar(er)
0 kommentar(er)
